2 tam giác đồng dạng là kiến thức quan trọng trong môn hình học lớp 8. Nó có liên quan đến nhiều dạng bài tập khác nhau. Cùng chúng tôi tìm hiểu chi tiết về định nghĩa, tính chất, các dạng tam giác đồng dạng,… qua những thông tin chia sẻ trong bài viết ngay sau đây.

2 tam giác đồng dạng là gì?

Khái niệm 2 tam giác đồng dạng: Hai tam giác gọi là đồng dạng với nhau nếu như chúng có ba cặp cạnh tương ứng tỉ lệ và ba cặp góc bằng nhau từng đôi một.

Tam giác ABC được gọi là đồng dạng với tam giác DEF nếu như:

Các góc: A = D; B = E; C = F và tỉ lệ của các cạnh: AB/DE = BC/EF = AC/DF

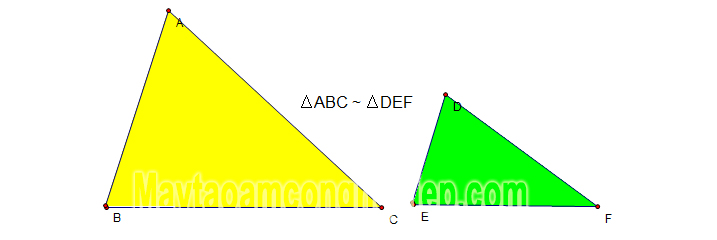
Ký hiệu đồng dạng được quy ước là dấu ∼ ngược. Nếu như tam giác ABC đồng dạng với tam giác DEF thì ta sẽ có ký hiệu là: △ABC ∼ △DEF.

Gọi tỉ lệ DE/AB = EF/BC = DF/AC = k. Trong trường hợp này, k sẽ được gọi là tỉ số đồng dạng.

Định lý về 2 tam giác đồng dạng được thể hiện như sau: Nếu như một đường thẳng cắt hai cạnh của tam giác đồng thời song song với cạnh còn lại thì nó tạo ra một tam giác mới đồng dạng với tam giác đã cho.

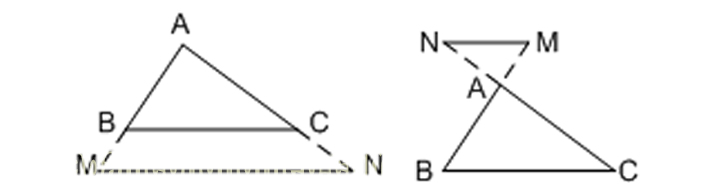
Ví dụ, cho ΔABC có M thuộc AB, N thuộc AC và MN // BC

=>ΔAMN ~ ΔABC

Chú ý: Định lí này cũng đúng ở trong trường hợp đường thẳng cắt phần kéo dài hai cạnh của tam giác đồng thời song song với cạnh còn lại.

Các trường hợp đồng dạng của hai tam giác

Thực tế thì có nhiều trường hợp tam giác đồng dạng khác nhau. Cụ thể, hai tam giác đồng dạng được chia thành 3 trường hợp đồng dạng khác nhau, đó là cạnh – cạnh – cạnh, cạnh – góc – cạnh và góc – góc – góc.

Trường hợp 2 tam giác đồng dạng cạnh – cạnh – cạnh

2 tam giác được gọi là đồng dạng với nhau nếu như ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.

Ví dụ: Tam giác ABC có 3 cạnh lần lượt là 6,8,10 và tam giác DE’ có 3 cạnh là 3,4,5. Ta thấy 2 tam giác này có tỉ lệ 6/3=8/4=10/5 cho nên tam giác ABC và tam giác DEF là 2 tam giác đồng dạng.

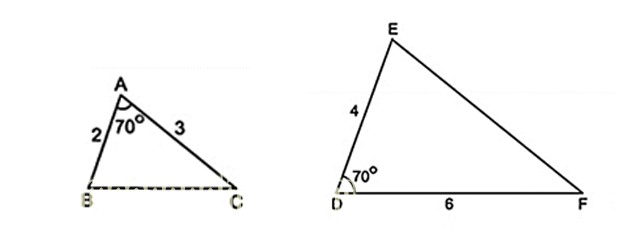
Trường hợp 2 tam giác đồng dạng cạnh – góc – cạnh

Nếu như 2 cạnh của tam giác này tỉ lệ với 2 cạnh của tam giác kia và 2 góc tạo bởi các cặp cạnh đó bằng nhau thì 2 tam giác này đồng dạng với nhau.

Ví dụ: Tam giác ABC có AB = 3cm, BC = 4cm và góc ABC = 60 độ. Tam giác M’N’P’ có M’N’ = 6cm, N’P’ = 8cm và góc M’N’P’ = 60 độ. Do đó mà 2 tam giác này đồng dạng với nhau.

Trường hợp 2 tam giác đồng dạng góc – góc – góc

Trường hợp 2 tam giác đồng dạng góc – góc – góc được hiểu là nếu như hai góc của tam giác này lần lượt bằng với hai góc của tam giác kia thì hai tam giác đó sẽ đồng dạng với nhau.

Ví dụ: Tam giác MNP có góc MNP = 40 độ, NPM = 50 độ và tam giác DEF có góc DEF = 40 độ, EDF’ = 50 độ thì 2 tam giác này được xem là đồng dạng với nhau.

Tính chất của 2 tam giác đồng dạng

Xét về tính chất của 2 tam giác đồng dạng, thì ta có những tính chất như sau:

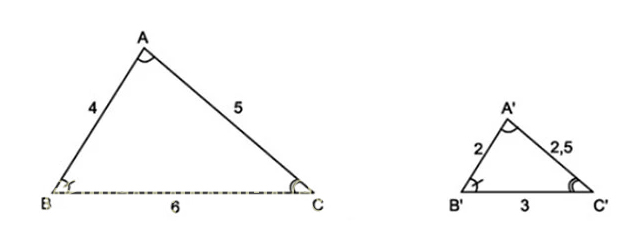
• Trong các tam giác đồng dạng thì các góc tương ứng bằng nhau.
• Các cạnh tương ứng của các tam giác đồng dạng có cùng tỷ lệ.
• Mỗi một tam giác đều đồng dạng với chính tam giác đó.
• Nếu như tam giác ABC đồng dạng với tam giác A’B’C’ thì ngược lại tam giác A’B’C’ cũng sẽ đồng dạng với tam giác ABC.
• Trong trường hợp mà 2 tam giác đều cùng đồng dạng với 1 tam giác bất kỳ thì 2 tam giác đều này cũng đồng dạng với nhau. Ví dụ: △ABC ∼ △A’B’C’, mà △A”B”C” ∼ △A’B’C’, thì ta có △ABC ∼ △A”B”C”
• Ngoài ra, nếu như hai tam giác bất kỳ bằng nhau thì chúng cũng sẽ đồng dạng với nhau. Nhưng 2 tam giác đồng dạng với nhau thì không phải lúc nào cũng có kích thước bằng nhau.
• Các hình tam giác đồng dạng thì có hình dạng giống nhau nhưng có thể có kích thước khác nhau.
• Tỉ số diện tích của các tam giác đồng dạng bằng tỉ số bình phương của bất kỳ cặp cạnh tương ứng nào.

Cách chứng minh 2 tam giác đồng dạng

Để có thể chứng minh 2 tam giác đồng dạng thì bạn có thể áp dụng một trong bốn cách sau:

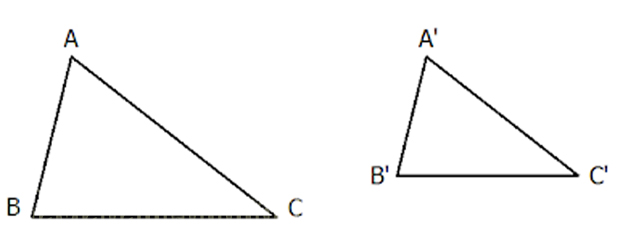
Cách 1: Hãy dựa vào 1 trong 3 trường hợp đồng dạng của tam giác để tiến hành chứng minh. Cụ thể trong trường hợp hình ảnh trên là cạnh – cạnh – cạnh. Hai tam giác được coi là đồng dạng nếu như chúng có các cặp cạnh tương ứng tỉ lệ.

Cách 2: Chứng minh theo định lý Talet: Nếu như một đường thẳng song song với một cạnh của tam giác đồng thời cắt hai cạnh còn lại thì nó sẽ tạo ra trên cạnh đó các đoạn thẳng tương ứng tỷ lệ.

Cách 3: Cần chứng minh những điều kiện cần và đủ theo định nghĩa: hai tam giác có những cặp cạnh tương ứng tỉ lệ thì sẽ đồng dạng. Hai tam giác mà có hai cặp góc tương ứng bằng nhau thì sẽ đồng dạng, hai góc xen giữa hai cặp cạnh ấy bằng nhau thì sẽ đồng dạng.

Cách 4: Chứng minh 2 tam giác đồng dạng theo trường hợp cạnh-góc-cạnh. 2 tam giác được coi là đồng dạng với nhau nếu 2 cạnh của tam giác này tỷ lệ cùng với 2 cạnh của tam giác kia và 2 góc tạo bởi tạo những cặp cạnh đó bằng nhau.

Bài tập minh họa về 2 tam giác đồng dạng

Sau khi đã hiểu hơn về 2 tam giác đồng dạng, hãy cùng tham khảo một số bài tập sau đây để có thể nắm vững kiến thức hơn.

Bài tập 1: Cho ΔABC cân tại A có BC = 2a. Gọi M chính là trung điểm của cạnh BC. Trên AB, AC lần lượt lấy  các điểm D; E sao cho góc DME = góc ABC

a) Chứng minh: ΔBDM ∽ ΔCME

b) Chứng minh rằng ΔMDE ∽ ΔDBM

c) Chứng minh rằng BD.CE không đổi

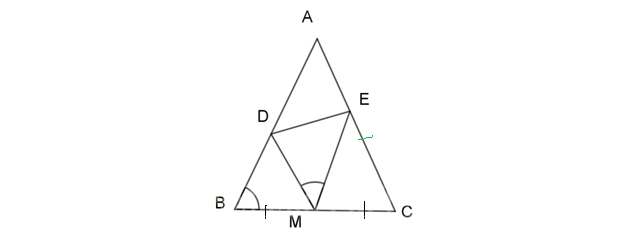
a) Theo giải thiết ta có góc MBD = góc MCE vì ΔABC cân tại A (1) và có góc DBM = góc DCM.

Theo lý thuyết tổng 3 góc trong tam giác luôn bằng 180 độ. Cho nên góc DBM + góc BMD + góc MDB =180.

EMD + DMB + EMC =180०

Suy ra góc BDM = góc EMC (2)

Từ (1) và (2), ta có ΔBDM ∽ ΔCME (g.g.g).

b) Vì ΔBDM ∽ ΔCME

Cho nên cạnh BD/CM=DM/ME và BM = CM (theo gt)

BD/BM = DM/ME => ΔMDE ∽ ΔDBM.

c) Vì ΔBDM ∽ ΔCME

Cạnh BD/CM = BM/CE

Cho nên CE.DB=BM.CM

Mà BM=CM=BC/2= a ⇒ BD.CE = CM.BM = a2

Bài tập 2: Cho ΔPQR có góc PQR = 70 độ, góc QPR = 60 độ và ΔXYZ có góc YXZ = 60 độ và XZY = 50 độ. Hãy kiểm tra xem hai tam giác này có đồng dạng với nhau hay không.

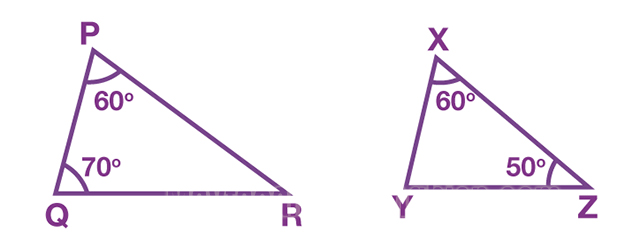
Lời giải

Trong tam giác PQR tổng 3 góc luôn bằng 180 độ, ta có:

QPR + PQR + QRP = 180° ⇔ 60° + 70° + QRP = 180°

=> 130° + QRP = 180° => QRP = 180° – 130° = 50°

Chúng ta có góc QRP = 50°

Xét trong tam giác XYZ, theo tính chất tổng các góc trong tam giác ta có:

YXZ + XYZ + XZY = 180° ⇔ 60° + XYZ + 50°= 180°

=> 110° + XYZ = 180° => XYZ = 180° – 110° = 70°

Chúng ta có góc XYZ = 70°

Do đó, theo trường hợp 2 tam giác đồng dạng góc-góc-góc thì ΔPQR~ΔXYZ.

Bài tập 3: Trong ∆ABC có cạnh BC = 20cm, trên cạnh AB lấy điểm P sao cho PA có độ dài là 5cm, PB = 10cm. Ngoài ra cạnh PQ||BC. Tìm cạnh PQ.

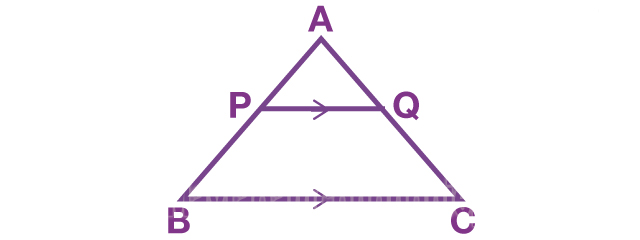
Lời giải

Trong ΔABC và ΔAPQ, góc PAQ là chung và góc APQ = góc ABC (các góc tương ứng)

⇒ ΔABC ~ ΔAPQ

⇒ AP/AB  =  PQ/BC

⇒ 5/15 = PQ/20

⇒ PQ = 20/3cm

Trên đây là những thông tin khái lược về 2 tam giác đồng dạng. Đây là kiến thức rất quan trọng, có ảnh hưởng đến nhiều dạng bài tập khác nhau. Do đó bạn cần phải nắm vững những kiến thức này nhé. Hy vọng những chia sẻ trên đây có thể giúp ích cho bạn.

>>>> Xem thêm bài viết Hình thoi là gì? Dấu hiệu nhận biết, công thức tính chu vi, diện tích hình thoi