Tiếp tuyến là một trong những kiến thức quan trọng trong chương trình Toán học lớp 9. Vậy tiếp tuyến là gì? Tiếp tuyến có tính chất gì? Làm thế nào để nhận biết được tiếp tuyến? Tất cả những thắc mắc này sẽ được maytaoamcongnghiep.com chia sẻ chi tiết trong bài viết dưới đây, đừng bỏ lỡ nhé!
Khái niệm tiếp tuyến là gì lớp 9?

Tiếp tuyến là gì tiếp điểm là gì? – Tiếp tuyến là đường thẳng chỉ tiếp xúc với đồ thì mà không cắt đồ thị tại 1 điểm nhất định và điểm đó chính là tiếp điểm.
Tiếp tuyến của 1 đường cong tại 1 điểm bất kì thuộc đường cong là 1 đường thẳng và chỉ “chạm” vào đường cong đó tại điểm đó. Leibniz đã định nghĩa tiếp tuyến như 1 đường thẳng nối 1 cặp điểm gần nhau vô hạn trên đường cong. Chính xác hơn, 1 đường thẳng là 1 tiếp tuyến của đường cong y = f (x) tại điểm x = c trên đường cong, khi đường thẳng đó đi qua điểm (c, f (c)) trên đường cong, và độ dốc f ‘(c) với f ‘ là đạo hàm của f..
Công dụng của tiếp tuyến là gì? – Trong thực tế, tiếp tuyến rất có ích khi vận dụng để xác định độ dốc hoặc hệ số góc của 1 đường tại 1 điểm nhất định dọc theo hướng đó.
Tính chất của đường tiếp tuyến là gì?
Dưới đây là một số tính chất quan trọng của tiếp tuyến mà bạn cần ghi nhớ:
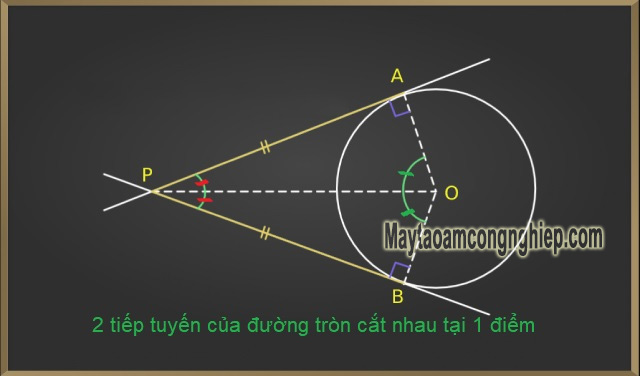
- Tiếp tuyến của đường tròn là đường thẳng vuông góc, đầu mút bán kính sẽ nằm trên đường tròn. Ngược lại, nếu đường thẳng vuông góc với bán kính tại điểm giao nhau giữa đường tròn và bán chính thì đó chính là tiếp tuyến.
- Đường thẳng vuông góc với tiếp tuyến tại điểm tiếp xúc với đường tròn sẽ đi qua tâm.
- Từ 1 điểm nằm ngoài đường tròn ta luôn vẽ được 2 tiếp tuyến với đường tròn đó.
- 2 tiếp tuyến của đường tròn sẽ cắt nhau tại điểm bất kỳ, điểm đó sẽ có khoảng cách cách đều 2 tiếp điểm. Theo đó, tia kẻ từ điểm cắt nhau đi qua tâm đường tròn sẽ được gọi là tia phân giác góc tạo bởi 2 tiếp tuyến. Còn tia kẻ từ tâm đi qua điểm cắt nhau sẽ gọi là tia phân giác của 2 bán kính đi qua tiếp điểm.
- Nếu 2 tiếp tuyến tại điểm A và B với đường tròn tâm O cắt nhau tại P thì góc BOA và góc APB bù nhau.
Dấu hiệu nhận biết tiếp tuyến đường tròn là gì?
Dưới đây là dấu hiệu nhận biết đường thẳng là đường tiếp tuyến:

- Nếu 1 đường thẳng đi qua 1 điểm nào đó nằm trên đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng đó chính là tiếp tuyến của đường tròn.
- Nếu 1 đường tròn và 1 đường thẳng chỉ có duy nhất 1 điểm chung thì đường thẳng đó sẽ là tiếp tuyến của đường tròn.
- Nếu khoảng cách từ tâm đường tròn đến đường thẳng bất kỳ bằng bán kính r của đường tròn thì đường thẳng đó sẽ là tiếp tuyến của đường tròn.
Góc tạo bởi dây cung và tia tiếp tuyến là gì?
Dây cung là gì? – Dây cung là đoạn thẳng có 2 đầu mút nằm trên đường tròn. Dưới đây là những tính chất của dây cung đường tròn:

- Các dây cung đều cách đều tâm khi chúng có chiều dài bằng nhau
- Đường trung trực của dây cung sẽ đi qua tâm đường tròn
- Trường hợp 2 góc cùng nằm trên 1 đường tròn chắn 2 dây cung bằng nhau hoặc cùng 1 dây cung thì chúng sẽ có số đo bằng nhau.
- Trong trường hợp cả 2 đường thẳng chứa dây cung AB và CD cùng thuộc 1 đường tròn cắt nhau tại điểm P, ta gọi chúng là 2 cát tuyến và có hệ thức PA.PB = PC.PD (tính chất phương tích của 1 điểm).
Góc tạo bởi tia tiếp tuyến và dây cung kết hợp với nhau sẽ tạo thành góc có đỉnh nằm trên đường tròn. Trong đó, 1 cạnh của góc này sẽ chứa tiếp tuyến và cạnh còn lại sẽ chứa dây cung của đường tròn đó.
- Định lý: Số đo của góc tạo bởi dây cung đường tròn với tia tiếp tuyến sẽ được xác định bằng ½ góc của cung bị chắn.
- Hệ quả: Trong một đường tròn, góc được tạo bởi tia tiếp tuyến và dây cung có số đo góc bằng với góc nội tiếp cùng chắn dây cung đó.
Phương trình tiếp tuyến của đồ thị hàm số
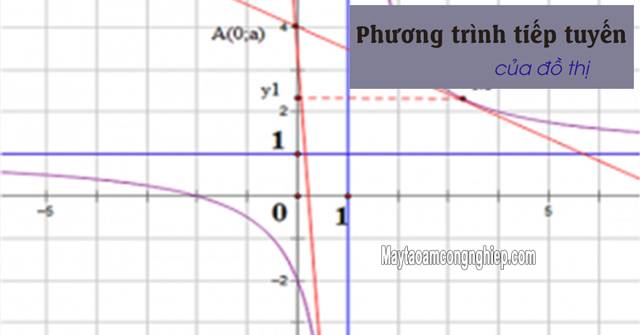
Phương trình tiếp tuyến là gì?
PT tiếp tuyến là gì? – Tiếp tuyến của đồ thị hàm số tại 1 điểm chính là 1 đường thẳng tiếp xúc trực tiếp với đồ thị hàm số tại chính điểm đó. Chúng ta có thể xác định được tiếp tuyến với đồ thị hàm số tại 1 điểm M(x0; y0) sẽ là: y=f′(x0).(x−x0)+f(x0).
Hệ số góc của tiếp tuyến là gì?
Dựa trên công thức trên, ta có thể thấy đạo hàm bậc nhất của hàm số tại hoành độ của điểm chính là hệ số góc của đường tiếp tuyến, tức là f′(x0) là hệ số góc của tiếp tuyến tại M(x0;y0).
Hướng dẫn cách viết phương trình tiếp tuyến
Trong các bài tập về tiếp tuyến đồ thị hàm số, để tìm được tiếp tuyến thì điểm mấu chốt là ta cần phải được điểm tiếp xúc hoặc giá trị của x0 trong công thức trên. Dưới đây là 1 số cách viết phương trình tiếp tuyến thường gặp:
PTTT vuông góc với đường thẳng
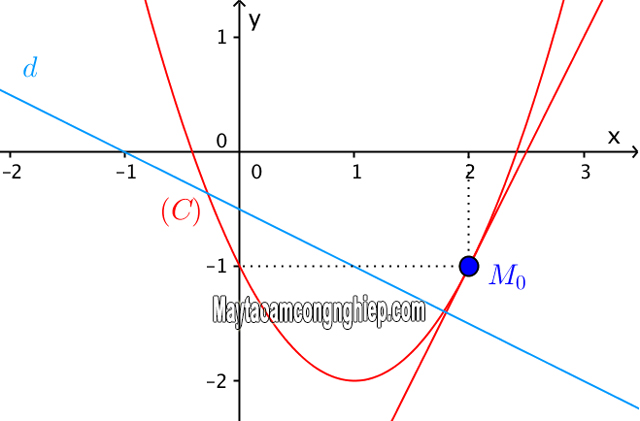
Tiếp tuyến (d) sẽ vuông góc với đường thẳng Δ ta sẽ có y = ax + b => ka = -1 => k = -(1/a).
Tóm lại: Phương trình tiếp tuyến d sẽ vuông góc với đường thẳng cho trước với hệ số góc k = -(1/k).
PTTT song song với đường thẳng
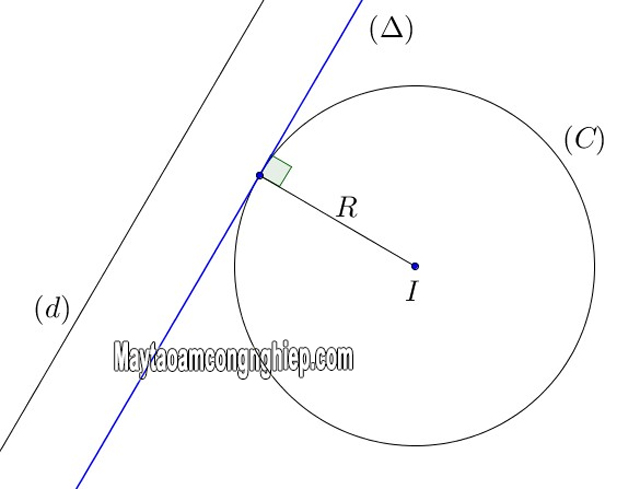
Tiếp tuyến d song song với đường thẳng Δ: y = ax + b => k = a.
Tóm lại: Phương trình tiếp tuyến d sẽ song song với các đường thẳng cho trước có hệ số góc là k = a.
Sau khi đã lập được phương trình tiếp tuyến thì các bạn cần nhớ kiểm tra lại tiếp tuyến đó có trùng với đường thẳng d không. Nếu trùng thì chúng ta sẽ không nhận kết quả đó.
Phương trình TT tại điểm
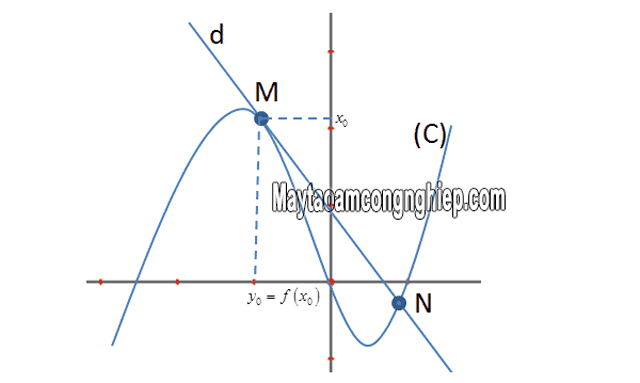
Để viết phương trình tiếp tuyến tại điểm chúng ta cần thực hiện theo các bước sau:
– Tính đạo hàm y’=f(x), từ đó tính được hệ số góc tiếp tuyến k=y’(x0)
– Lúc này ta sẽ có phương trình tiếp tuyến của đồ thị hàm số (C) tại M (x0, y0) có dạng là y= y’(x0)(x – x0) + y0.
Lưu ý:
- Khi đề bài cho hoành độ tiếp điểm x0 thì bạn cần tìm được y0 bằng cách thay thế điểm x0 vào hàm số y = f(x0).
- Nếu đề bài cho tung độ của tiếp điểm y0 thì cần tìm y0 bằng cách thế y0 vào hàm số y = f(x0).
- Trong trường hợp đề bài yêu cầu viết PTTT tại các giao điểm của đồ thị hàm số C: y = f(x) với d là: y = ax + b thì khi đó các hoành độ tiếp điểm x chính là nghiệm của phương trình hoành độ giao điểm giữa d với hàm số C. Và phương trình hoành độ giao điểm C và d sẽ có dạng là f(x) = ax + b.
- Đặc biệt, nếu trục hoành Ox thì sẽ có y = 0, trục tung Oy sẽ có x=0.
Nhận xét: Việc sử dụng máy tính để lập PTTT tại 1 điểm thực chất chỉ là cách rút gọn các bước ở cách tính thủ công. Ngoài ra, các bạn có thể sử dụng máy tính để tính toán và kiểm tra kết quả xem có chính xác không.
Dạng bài tập về PTTT của đồ thị hàm số
Dưới đây là một số dạng bài tập cơ bản về pt tiếp tuyến của đồ thị hàm số để củng cố kiến thức, các bạn có thể tham khảo

Dạng 1: Viết PTTT tại điểm M0(x0;y0) ∈ (C)
Gợi ý:
Để viết phương trình tiếp tuyến tại 1 điểm thì các bạn cần thực hiện theo các bước sau:
– Gọi M (x0; f(x0)) là tiếp điểm, sau đó tính hệ số góc tiếp tuyến k = f’(x0) dựa theo x0.
– Phương trình tiếp tuyến sẽ có dạng: y = f’(x0)(x – x0) + f(x0).
Do điểm A (xA; yA) thuộc d nên yA=f’(x0)(xA – x0) + f(x0), giải phương trình trên ta sẽ tìm được x0.
– Thay giá trị x0 vừa tìm được vào phương trình ta sẽ có được phương trình tiếp tuyến cần tìm.
Dạng 2: Biết trước hoành độ tiếp điểm x0, viết pt tiếp tuyến
Gợi ý:
– Tính đạo hàm hàm số, sau đó thay x0 vào ta sẽ được hệ số góc
– Thay x0 vào hàm số ta sẽ tìm được giá trị tung độ tiếp điểm
– Áp dụng phương trình y = k(x – x0) + y0 ta sẽ tìm được phương trình tiếp tuyến cần tìm.
Dạng 3: Cho trước hệ số góc tiếp tuyến k = y’(x0) = f’(x0)
Gợi ý:
– Thực hiện tính đạo hàm và giải phương trình: k = y’(x0) = f’(x0) để tìm giá trị x0
– Thay x0 vào hàm số ta sẽ có được tung độ tiếp điểm cần tìm.
Lưu ý, kết quả trả về có bao nhiêu giá trị của x0 thì sẽ có bấy nhiêu tiếp tuyến.
Dạng 4: Cho trước tung độ tiếp điểm y0
Gợi ý:
– Giải phương trình y0 = f(x0) để tìm giá trị của x0
– Tính đạo hàm hàm số và thay x0 vào ta được hệ số góc.
– Áp dụng y = k(x – x0) + y0 ta sẽ được phương trình tiếp tuyến cần tìm
Lưu ý: Khi có bao nhiêu giá trị của x0, khi thay vào ta sẽ có bấy nhiêu tiếp tuyến.
Lưu ý quan trọng khi làm bài tập tiếp tuyến đường tròn
Trong quá trình làm bài tập tiếp tuyến, các bạn cần lưu ý một số điều sau:

- Nắm vững định lý và tính chất có liên quan đến tiếp tuyến đường tròn
- Ghi chú, tóm tắt lại thành hệ thống các dữ liệu trong đề bài, tránh để sót thông tin.
- Đọc kỹ đề bài để nắm vững các thông tin
- Thường xuyên làm thêm các bài tập để rèn luyện, củng cố kiến thức
- Sử dụng máy tính cầm tay khi cần thiết để kiểm tra đáp án.
Một số thuật ngữ khác liên quan đến tiếp tuyến
Ngoài các thuật ngữ trên thì các bạn cũng cần nắm được một số thuật ngữ khác liên quan đến tiếp tuyến khác như:
Gia tốc tiếp tuyến là gì?
Gia tốc tiếp tuyến là đại lượng được sử dụng để mô tả cho sự thay đổi độ lớn của vectơ vận tốc. Gia tốc tiếp tuyến có những điểm lưu ý sau:
- Phương của gia tốc tiếp tuyến trùng với phương của tiếp tuyến
- Chuyển động nhanh dần khi cùng chiều và chuyển động chậm dần khi ngược chiều.
Ứng suất tiếp tuyến là gì?
Ứng suất tiếp tuyến hay ứng suất lực cản/ áp suất là ứng suất chỉ xuất hiện bên trong hệ do nội lực gây ra trên 1 đơn vị diện tích.
Lực tiếp tuyến là gì?
Lực tiếp tuyến cũng giống như tên gọi của nó theo phương tiếp tuyến và nó có tác dụng làm thay đổi độ lớn của vận tốc. Còn lực pháp tuyến hay lực hướng tâm có tác dụng làm thay đổi phương của vận tốc, nghĩa là làm cho chất điểm chuyển động theo quỹ đạo cong.
Bài viết trên đây chúng tôi đã cung cấp kiến thức tới bạn đọc về Tiếp tuyến là gì? Tính chất của tiếp tuyến và các dạng bài tập về tiếp tuyến thường gặp. Hy vọng những chia sẻ trên sẽ giúp các bạn học sinh có thêm kiến thức để áp dụng vào bài tập. Và nếu còn thắc mắc nào cần giải đáp, hãy để lại bình luận dưới bài viết này để mọi người hỗ trợ giải đáp nhé!

![[TỔNG HỢP]: Lời chúc ngày Thầy thuốc Việt Nam 27 2 hay nhất](https://maytaoamcongnghiep.com/wp-content/uploads/2024/02/ngay-thay-thuoc-Viet-Nam-27-2.20-150x150.jpg)



