Talet là gì? Talet là một định lý về tỷ lệ quan trọng trong hình học, đặc biệt là tam giác. Vì vậy chúng ta cần nắm rõ về quy tắc hình học này, sử dụng thành thạo để giải các bài toán liên quan. Để tìm hiểu chi tiết hơn về định lý Talet là gì? Cũng như hệ quả của định lý Talet, mời bạn đọc tham khảo bài viết sau.

Talet là gì?

Theo Wikipedia, định lý Thales (hay Định lý Talet) là một định lý rất quan trọng trong hình học, được đặt theo tên nhà toán học người Hy Lạp Thales. Thales of Miletus là nhà triết học đầu tiên của Hy Lạp cổ đại.

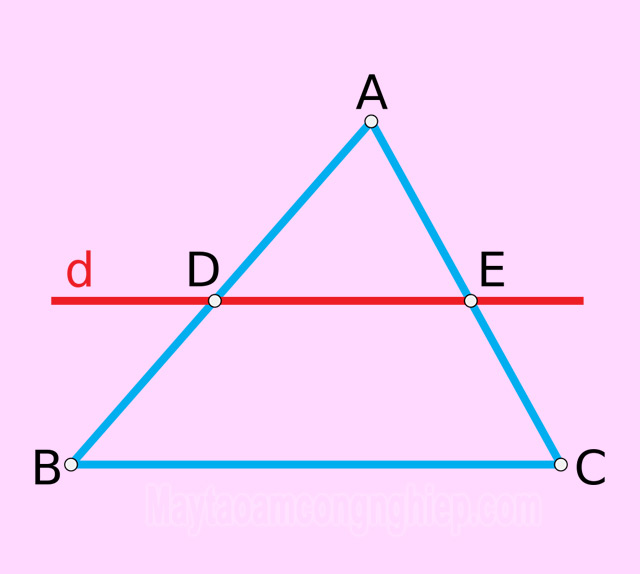
Trong tam giác, định lý Talet có tính hai chiều:

Định lý Talet thuận

Một đường thẳng song song với một cạnh của tam giác đó, đồng thời cắt hai cạnh còn lại thì sẽ định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Ví dụ: Tam giác ABC có đường thẳng (d) cắt AB tại D, cắt AC tại E và song song với BC.

=> Theo định lý Talet ta có:  và  và .

Định lý Talet đảo

Nếu một đường thẳng bất kỳ cắt hai cạnh của tam giác và định ra trên hai cạnh này những đoạn thẳng có tỉ lệ tương ứng, thì đường thẳng đó song song với cạnh còn lại của tam giác.

Ví dụ: Tam giác ABC,  hoặc  hoặc .

=> Theo định lý Talet đảo, ta có: DE song song với BC (DE // BC).

Những hệ quả talet là gì?

Trong phần này, chúng ta sẽ phân tích về ba hệ quả của định lý Talet (định lý Talet mở rộng).

• Hệ quả 1 định lý Talet: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại, sẽ tạo ra tam giác có ba cạnh tỉ lệ với ba cạnh của tam giác đã cho.
• Hệ quả 2 định lý Talet: Có một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại, sẽ tạo ra một tam giác mới đồng dạng với tam giác đã cho trước đó.
• Hệ quả 3 định lý Talet mở rộng: Ba đường thẳng đồng quy, chắc chắn trên hai đường thẳng sẽ song song các cặp đoạn thẳng tỉ lệ.

Định lý Talet trong hình học khác

Ngoài định lý Talet trong tam giác, chúng ta có thể áp dụng định lý Talet trong hình thang và không gian. Cụ thể như sau:

Định lý Talet trong hình thang

Nếu một đường thẳng song song với hai cạnh đáy của hình thang, đồng thời cắt hai cạnh bên của hình thì sẽ định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.

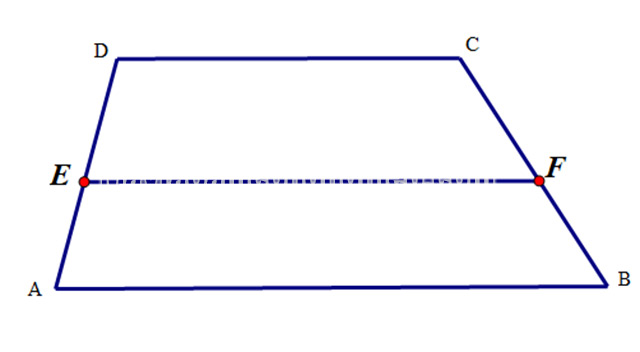
Cho hình thang ABCD, E thuộc AD và F thuộc BC

Nếu EF // AB // CD, ta có  .

Ngược lại, trường hợp , suy ra EF // AB // CD.

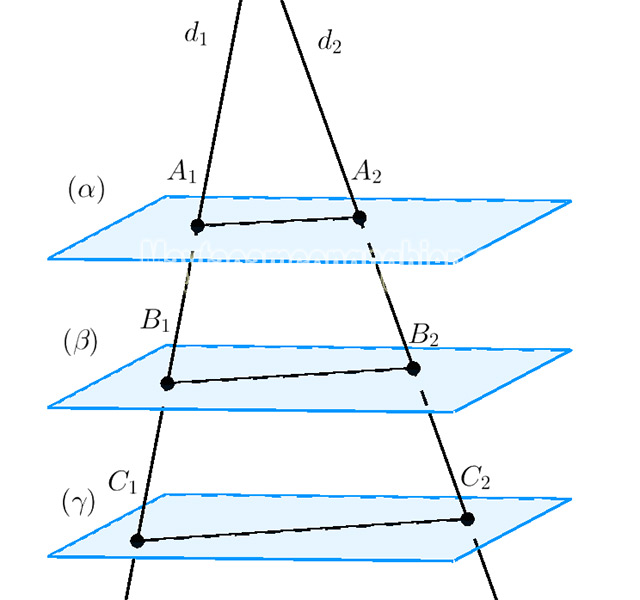
Định lý Talet trong không gian

Khi ba mặt phẳng trong không gian song song với nhau, chúng sẽ chắn các đoạn thẳng có tỉ số tương ứng trên hai đường thẳng đó. Ngoài ra, người ta còn phát triển định lý nghịch đảo của định lý Talet trong không gian như sau:

Với hai đường thẳng d₁ và d₂ cắt nhau thì điểm A₁, B₁, C₁ ∈ (d₁) và A₂, B₂, C₂ ∈ (d₂). Khi đó các đường thẳng A₁A₂, B₁B₂, C₁C₂ sẽ cùng song song với  một mặt phẳng.

Ứng dụng của Talet trong thực tiễn

Định lý Talet được áp dụng trong nhiều lĩnh vực khác nhau, như hình học, cơ học, và thiết kế. Dưới đây sẽ là một số ứng dụng cụ thể của định lí Talet:

• Trong kiến trúc và thiết kế: Talet giúp các kiến trúc sư và nhà thiết kế xác định các góc và tỉ lệ của các hình khối trong công trình kiến trúc, đảm bảo tính cân đối. Ví dụ, định lý Talet được dùng để xác định các góc và tỉ lệ của các cánh cửa và cửa sổ trong một ngôi nhà.
• Trong địa hình và địa chất: Định lý Talet có thể xác định sự song song giữa các dãy núi, dòng sông và các yếu tố địa chất khác. Từ đó hỗ trợ việc phân tích và hiểu rõ các dạng địa hình và địa chất.
• Trong ngành xây dựng: Talet là gì được áp dụng trong việc tính toán và xác định độ dốc, kích thước và tỷ lệ các công trình xây dựng như cầu đường, cao tốc, hầm. Điều này nhằm đảm bảo tính an toàn và thẩm mỹ cho các công trình xây dựng.
• Trong vật lý và cơ học: Talet được ứng dụng để xác định sự song song và tỷ lệ giữa các đường thẳng trong bài tập vật lý và cơ học. Từ đó giúp giải quyết các bài toán liên quan đến vận tốc, tốc độ, gia tốc của vật thể.
• Trong nghệ thuật và thiết kế đồ họa: Định lý Talet được sử dụng để tạo ra các tác phẩm nghệ thuật, thiết kế đồ họa. Giúp việc chọn lựa và sắp đặt các yếu tố hình học để tạo nên những tác phẩm thẩm mỹ.

Áp dụng Talet vào việc đo đạc kích thước của vật

Định lý Talet được áp dụng rất nhiều vào thực tiễn. Đơn giản nhất là công việc đo đạc kích thước của một vật rộng lớn (con người không thể đo trực tiếp).

Đo khoảng cách giữa 2 bờ sông: Talet là gì được áp dụng để đo khoảng cách giữa 2 bờ sông mà không cần phải đi sang sông.

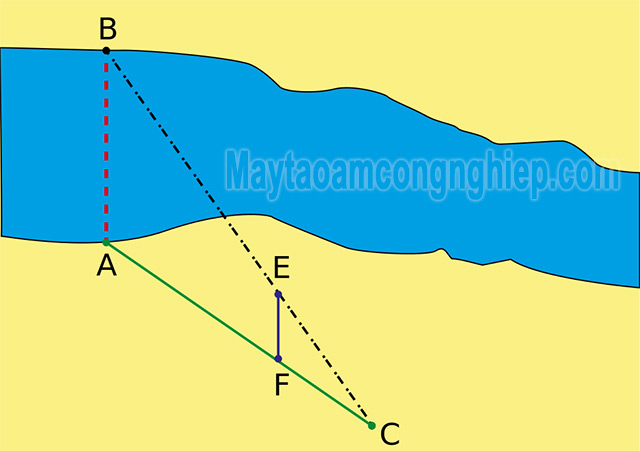
Các bước thực hiện như sau:

• Bước 1: Đánh dấu hai điểm khoảng cách cần đo là A và B, chọn vị trí đứng ở điểm C bất kỳ.
• Bước 2: Lấy hai điểm E, F sao cho EF // AB. Muốn EF // AB, cần tiến hành đo góc , lấy góc  = .
• Bước 3: Đo AC, FC, EF và tính AB theo công thức sau: .

Đo chiều cao của một vật: Chúng ta cũng có thể áp dụng định lý Thales kết hợp với bóng mặt trời để đo chiều cao vật.

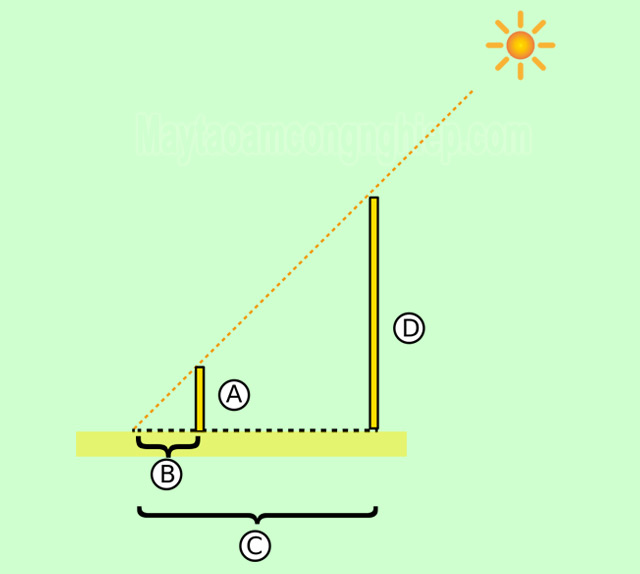
Các bước thực hiện như sau:

• Bước 1: Bố trí hình vẽ, với D là chiều cao vật cần đo, C là chiều dài bóng của vật, A là chiều cao cây cột và B là chiều dài bóng của cây cột đó.
• Bước 2: tiến hành đo A, B, C
• Bước 3: Tính toán và tìm D theo công thức sau: .

Bên trên là những thông tin giải đáp cho câu hỏi Talet là gì mà chúng tôi muốn chia sẻ với bạn đọc. Hy vọng rằng bài viết này đã đem đến cho các bạn những kiến thức bổ ích. Từ đó hiểu rõ hơn về định lý Talet và áp dụng thành thạo vào giải các bài tập có liên quan.

>>> Xem thêm bài viết: Tia đối là gì? Các dạng bài tập liên quan đến tia đối