Trong hình học, hình thoi là một hình tứ giác là phiên bản đặc biệt của hình bình hành. Tương tự như những loại hình học khác, hình thoi cũng sẽ có những đặc điểm, tính chất, công thức tính toán liên quan. Cùng tìm hiểu hình thoi là gì để hiểu rõ về hình tứ giác này nhé.

Hình thoi là gì?

Trong hình học Euclide, hình thoi là trường hợp đặc biệt của hình bình hành. Trong hình thoi, các cạnh đối diện song song và bằng nhau, các góc đối diện bằng nhau. Hai đường chéo của hình thoi luôn cắt nhau tại trung điểm của mỗi đường. Hình thoi còn được gọi là hình kim cương.

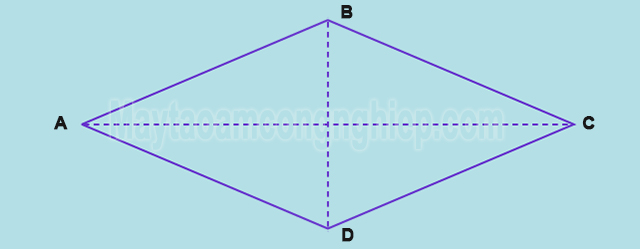
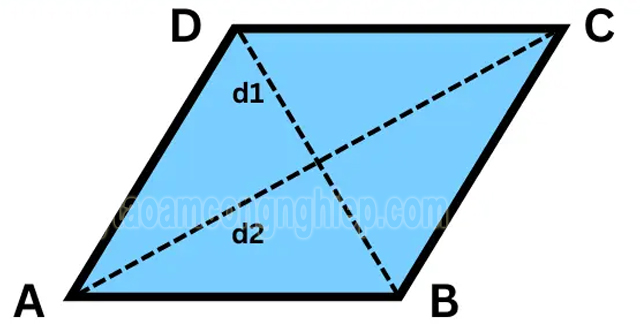
Trong hình trên, bạn có thể thấy hình thoi ABCD, trong đó AB, BC, CD và AD là các cạnh của hình thoi và AC và BD là các đường chéo của hình thoi.

Tính chất của hình thoi là gì?

Sau khi biết hình thoi là gì thì chúng ta cùng tìm hiểu về các tính chất của hình thoi. Trong một hình thoi luôn có:

• Hai góc đối bằng nhau.
• Các cạnh đối diện của hình thoi luôn song song với nhau.
• Hai đường chéo vuông góc với nhau và cắt nhau ở trung điểm của mỗi đường.
• Hai đường chéo là những đường phân giác các góc của hình thoi.
• Các đường chéo của hình thoi là 2 đường đối xứng duy nhất mà hình thoi có. Chúng chia hình thoi thành 2 nửa giống hệt nhau.
• Tổng hai góc kề nhau trong hình thoi bằng 180 độ.
• Tất cả các góc trong của hình thoi cộng lại bằng 360°.
• Bạn sẽ có được một hình chữ nhật khi nối điểm giữa của các cạnh.
• Bạn sẽ có được một hình thoi khác khi nối trung điểm của các đường chéo.
• Xung quanh hình thoi không thể có đường tròn ngoại tiếp.
• Trong một hình thoi không thể có đường tròn nội tiếp.
• Khi đường chéo ngắn hơn bằng một trong các cạnh của hình thoi thì hai hình tam giác đều bằng nhau sẽ được hình thành.

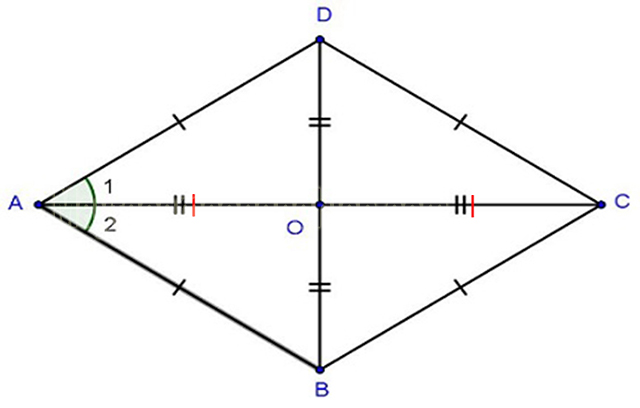
Dấu hiệu nhận biết hình thoi là gì?

Dựa vào tính chất của hình thoi, các nhà toán học đã đề ra nhiều dấu hiệu để nhận biết hình thoi từ hình tứ giác và hình bình hành, cụ thể như sau:

Hình tứ giác đặc biệt

• Hình tứ giác có bốn cạnh bằng nhau thì là hình thoi.
• Hình tứ giác mà có hai đường chéo là đường trung trực của nhau thì là hình thoi.
• Hình tứ giác có hai đường chéo là đường phân giác của cả bốn góc thì là hình thoi.

Hình bình hành đặc biệt

• Hình bình hành mà có hai cạnh kề bằng nhau thì là hình thoi.
• Hình bình hành mà có hai đường chéo vuông góc với nhau thì chính là hình thoi.
• Hình bình hành mà có hai đường chéo là đường phân giác của một góc thì là hình thoi.

Công thức tính chu vi hình thoi là gì?

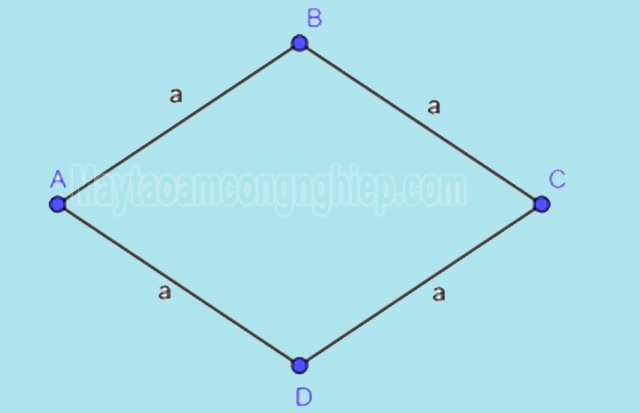
Chu vi của hình thoi được tính bằng tổng độ dài của các đường bao quanh hình. Nó cũng chính bằng độ dài của một cạnh nhân với 4.

P = a x 4

Trong đó:

• P: là chu vi hình thoi
• a: là cạnh hình thoi

Công thức tính diện tích hình thoi là gì?

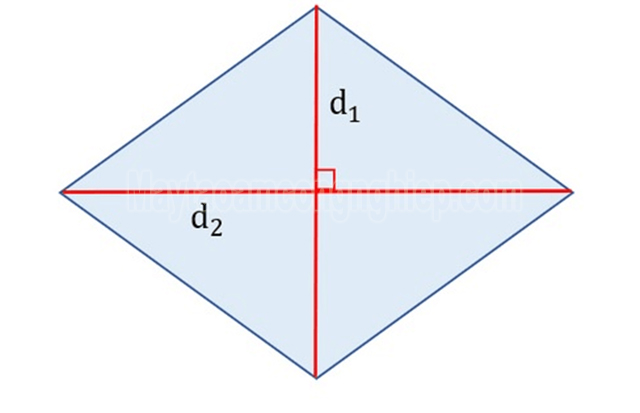
Diện tích của hình thoi được đo bằng độ lớn của bề mặt hình. Nó chính là phần mặt phẳng mà ta có thể nhìn thấy của hình thoi. Diện tích của hình thoi được tính bằng nửa tích độ dài của hai đường chéo hoặc bằng tích của chiều cao hình thoi với cạnh hình thoi.

S = ½ x (d1 x d2) hoặc = h x a

Trong đó:

• S: là diện tích hình thoi
• d1, d2: là hai đường chéo hình thoi
• h: là chiều cao của hình thoi
• a: là cạnh hình thoi

Một số bài tập về hình thoi

Cùng tham khảo một số bài tập sau đây để nắm chắc hơn về các kiến thức hình thoi.

Bài tập 1: Cho một hình thoi có độ dài hai đường chéo của hình thoi là 18 cm và 12 cm. Tìm diện tích hình thoi.

Lời giải:

Theo giải thiết có Đường chéo (d1) = 18 cm

Đường chéo (d2) = 12 cm

Diện tích hình thoi = ½(d1 x d2) = ½(18 x 12) = 108cm2

Bài tập 2: Tính chu vi của hình thoi có cạnh là 15cm.

Lời giải:

Độ dài cạnh hình thoi (a) = 15 cm

Chu vi hình thoi = 4 × a = 4 × 15 cm = 60 cm

Bài tập 3: Diện tích hình thoi là 56cm2. Biết độ dài một đường chéo của nó là 14cm. Hãy tìm độ dài đường chéo còn lại.

Lời giải:

Diện tích hình thoi = 56 cm2

d1 = 14cm

Ta biết diện tích hình thoi = ½(d1 x d2)

 ⇒ 56 = 1/2(14 x d2)

⇒ 56 = 7 × d2

⇒ d2 = 56/7

⇒ d2 = 8cm

Vì vậy, đường chéo thứ hai của hình thoi đã cho có kích thước 8 cm.

Đến đây hẳn bạn đã biết hình thoi là gì cũng như đặc điểm, tính chất, công thức tính của hình tứ giác này. Hy vọng những chia sẻ này sẽ giúp bạn giải quyết các bài tập dễ dàng hơn.

>>> Xem thêm bài viết: BaCl2 có kết tủa không? Tính chất, cách điều chế, ứng dụng BaCl2