Định lý Menelaus là kiến thức quan trọng có trong chương trình Toán lớp 9 và lớp 11. Đây là một trong những công cụ hữu ích giúp các bạn học sinh, sinh viên giải quyết tốt các bài toán về tam giác. Để nắm chắc hơn về định lý cũng như ứng dụng của định lý Menelaus, mời các bạn cùng tham khảo bài viết sau.

Định lý Menelaus là gì?

Định lý Menelaus là một định lý trong hình học Euclid, được đặt theo tên nhà toán học cổ Hy Lạp Menelaus of Alexandria. Theo Wikipedia, “Định lý Menelaus là một định lý cơ bản trong hình học tam giác, được phát biểu như sau: Cho tam giác ABC. Các điểm D, E, F lần lượt nằm trên các đường thẳng BC, CA, AB. Khi đó D, E, F thẳng hàng khi và chỉ khi: ”

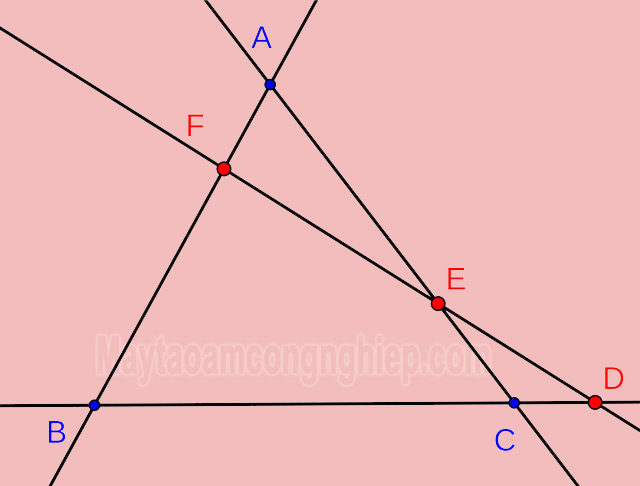
Định lý menelaus lớp 9 là một trong những kiến thức cơ bản giúp ta biết được mối quan hệ giữa các đường thẳng trong tam giác. Định lý này cũng có liên quan đến tỉ số của các đoạn thẳng trên một tam giác. Từ đó chúng ta sẽ biết được có bao nhiêu điểm nằm trên cùng một đường thẳng trong tam giác. Đồng thời xác định xem liệu tam giác đó có đồng quy hay không.

Chứng minh định lý Menelaus

Dưới đây là cách chứng minh định lý Menelaus:

Phần thuận

Giả sử 3 điểm D, E, F thẳng hàng với nhau. Vẽ đường thẳng đi qua điểm C và song song với đường thẳng AB, cắt đường thẳng DE tại điểm G.

Vì CG // AB nên theo định lý Talet ta có:  (1) và  (2)

Nhân (1) và (2) và vế theo vế ta có:  = => 

Phần đảo

Giả sử . Khi đó F’ được gọi là giao của đường thẳng ED với đường thẳng AB.

Theo chứng minh ở trên ta có  

Kết hợp giả thiết suy ra 

Hay 

Nên F’A = FA và F’B = FB  => F’ trùng với F

=> Vậy là định lý đã được chứng minh

Định lý Menelaus trong không gian áp dụng trong trường hợp nào?

Định lý Menelaus là một công cụ quan trọng trong hình học Euclid, được áp dụng trong việc chứng minh, tìm ra quy luật và giải các bài toán liên quan đến các hình học đa giác và tứ giác. Cụ thể như:

• Chứng minh tồn tại điểm sau cho ba đường thẳng: Định lý Menelaus được sử dụng để chứng minh rằng ba đường thẳng đi qua ba điểm thẳng hàng, tồn tại một điểm nằm trên cả ba đường thẳng đó.
• Chứng minh đường thẳng song song: Nếu áp dụng định lý Menelaus cho một tam giác với hai đường chéo giao nhau trên một đường thẳng. Ta có thể suy ra rằng những đường thẳng từ các đỉnh của tam giác đến các điểm trên đường chéo song song với đường thẳng thứ ba.
• Xác định tỷ lệ giữa các đoạn thẳng: Định lý Menelaus cũng có thể được sử dụng để tính tỷ lệ giữa các đoạn thẳng bên trong tam giác. Bằng cách áp dụng định lý này, ta có thể tính được tỷ lệ của các đoạn thẳng trong tam giác khi biết một số thông tin về đoạn thẳng khác.
• Ứng dụng trong hình học tứ giác: Định lý Menelaus cũng có thể được áp dụng trong việc chứng minh và tìm các quy luật liên quan đến hình học tứ giác. Với điểm lấy từ định lý Menelaus, ta có thể xây dựng các quy luật và giải các bài toán liên quan đến hình học tứ giác.

Cách áp dụng định lý Menelaus để giải bài toán liên quan đến tam giác

Định lý Menelaus là được xem công cụ hữu ích để giải quyết các bài toán liên quan đến tam giác. Để áp dụng định lý này, chúng ta thực hiện theo các bước sau đây.

• Bước 1: Đầu tiên cần vẽ đường thẳng đi qua một đỉnh của tam giác, đồng thời song song với cạnh đối diện với đỉnh đó.
• Bước 2: Tiếp theo vẽ hai đường thẳng khác song song với hai cạnh còn lại của tam giác, cắt đường thẳng ở bước 1 tại hai điểm.
• Bước 3: Khi đó đường thẳng qua hai điểm cắt trên hai cạnh tam giác sẽ tạo thành hai đoạn thẳng cắt nhau tại một điểm.
• Bước 4: Các đường thẳng và đoạn thẳng này sẽ tạo thành một tứ giác nội tiếp.
• Bước 5: Áp dụng định lý Menelaus để tính toán các tỷ lệ của các đoạn thẳng trong tứ giác nội tiếp này.
• Bước 6: Nếu biết một tỷ lệ của các đoạn thẳng trong tứ giác nội tiếp này, ta có thể tính toán tỷ lệ của các đoạn thẳng còn lại.

Đối với các bài toán liên quan đến tam giác, các bạn có thể áp dụng định lý Menelaus để tìm các tỷ lệ của các đoạn thẳng và tính toán các giá trị còn lại.

Ví dụ về bài tập định lý Menelaus lớp 11

Dưới đây là một số dạng bài tập liên quan đến định lý  Menelaus:

Bài tập 1: Cho tam giác ABC có nội tiếp đường tròn tâm (O). Tiếp tuyến A của (O) cắt đường thẳng BC tại D, tiếp tuyến tại B cắt AC tại E và tiếp tuyến tại C cắt AB tại F. Hãy chứng minh rằng 3 điểm D, E, F thẳng hàng với nhau.

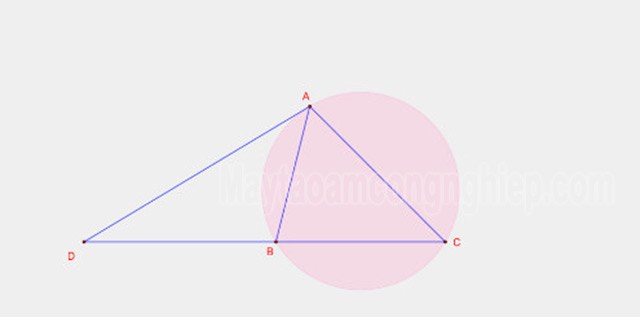
Gợi ý: Ta có . Suy ra 

=> .

Tương tự ta có: .

Khi đó: 

Bài tập 2: Cho tam giác ABC. M và N là các điểm thuộc cạnh AB, AC sao cho AM = MB, AN = 2NC.MN cắt đường thẳng BC tại P. Chứng minh CP = CB.

Gợi ý: Áp dụng định lý Menelaus cho tam giác ABC với ba điểm M, N, P thẳng hàng ta có: 

Ta đã có MA = MB, AN = 2NC. Suy ra  => PB = PC.

Ứng dụng của định lý Menelaus trong thực tiễn

Định lý Menelaus được ứng dụng trong nhiều lĩnh vực khác nhau như: kỹ thuật, công nghệ, vật lý và thiết kế.

• Trong lĩnh vực kỹ thuật: Định lý Menelaus thường được sử dụng để tính toán quỹ đạo của các vật thể di chuyển trong không gian. Các kỹ sư và nhà thiết kế cũng có thể áp dụng định lý Menelaus để tối ưu hóa các thiết kế máy bay, tàu thủy, các công trình xây dựng.
• Trong vật lý: Áp dụng định lý Menelaus vào việc tính toán về tốc độ và vận tốc của các vật thể di chuyển. Các nhà khoa học có thể áp dụng định lý Menelaus để giải quyết các bài toán về chuyển động, động lực học.
• Trong thiết kế: Định lý Menelaus cũng được sử dụng trong thiết kế đường dây điện và mạng lưới viễn thông. Các kỹ sư có thể áp dụng định lý này để dễ dàng tính toán được các thông số của hệ thống mạng lưới.

Trên đây là những thông tin tổng quan về định lý Menelaus trong không gian. Cùng với đó là cách ứng dụng định lý này vào giải bài tập toán có liên quan. Hy vọng, bài viết hữu ích này đã cung cấp thêm cho bạn nguồn tư liệu để bạn dạy và học tốt hơn.

>>> Xem thêm bài viết: Gia tốc là gì? Gia tốc kí hiệu là gì? Công thức tính gia tốc